1.
如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=∠DBO.
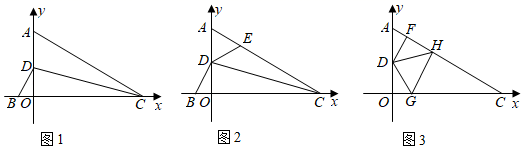
(1)
求证:AC=BC;
(2)
如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;
(3)
在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当H在FC上移动,点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
【考点】
全等三角形的应用;
三角形全等的判定-AAS;
能力提升




