1.
如图

(1)
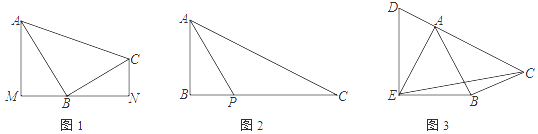
如图1,在△ABC中,  ,CD平分
,CD平分  ,交AB于点D,
,交AB于点D,  //
//  ,交BC于点E.
(2)
如图2,
,交BC于点E.
(2)
如图2,  和
和  是△ABC的2个外角,
是△ABC的2个外角,  ,CD平分
,CD平分  ,交AB的延长线于点D,
,交AB的延长线于点D,  //
//  ,交CB的延长线于点E.记△ACD的面积为
,交CB的延长线于点E.记△ACD的面积为  ,△CDE的面积为
,△CDE的面积为  ,△BDE的面积为
,△BDE的面积为  .若
.若  ,求
,求  的值.
的值.
①若 ,
,求BC的长;
②试探究 是否为定值.如果是,请求出这个定值;如果不是,请说明理由.
【考点】
等腰三角形的判定;
两条直线被一组平行线所截,所得的对应线段成比例;
相似三角形的判定与性质;
锐角三角函数的定义;
能力提升