1.
已知 是
是 的直径,点A,点B是
的直径,点A,点B是 上的两个点,连接
上的两个点,连接 , 点D,点E分别是半径
, 点D,点E分别是半径 的中点,连接
的中点,连接 , 且
, 且 .
.
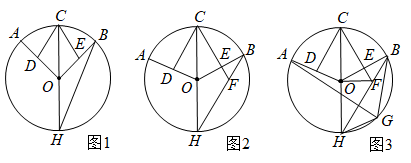
(1)
如图1,求证: ;
(2)
如图2,延长
;
(2)
如图2,延长 交
交 于点F,若
于点F,若 , 求证:
, 求证: ;
(3)
如图3,在(2)的条件下,点G是
;
(3)
如图3,在(2)的条件下,点G是 上一点,连接
上一点,连接 , 若
, 若 ,
,  , 求
, 求 的长.
的长.
【考点】
三角形全等及其性质;
等边三角形的判定与性质;
含30°角的直角三角形;
圆周角定理;
线段的中点;