1.
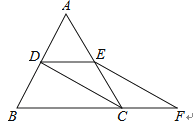
在等边 中,D,E,F分别是边AB,BC,CA上的动点,满足
中,D,E,F分别是边AB,BC,CA上的动点,满足 , 且
, 且 . 作点E关于AC的对称点G,连接CG,DG.
. 作点E关于AC的对称点G,连接CG,DG.

(1)
当点D,E,F在如图1所示的位置时,请在图1中补全图形,并证明四边形DBCG是平行四边形;
(2)
当 ,
,  时,求∠BDE的度数.
时,求∠BDE的度数.
【考点】
等边三角形的性质;
平行四边形的判定与性质;