0 返回出卷网首页
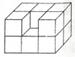
1. 如图是一个长3cm、宽与高都是2cm的长方体。将它挖掉一个棱长1cm的小正方体（如图），它的表面积（    ）

A. 比原来大 B. 比原来小 C. 不变 D. 无法确定
【考点】
组合体的表面积的巧算;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
单选题 普通
基础巩固
能力提升
变式训练
拓展培优
真题演练
换一批
1.  一个棱长是4厘米的正方体，从它的个顶点处挖去一个棱长是1厘米的小正方体后，剩下物体的表面积和原来的表面积相比较，（ ）
A. 变大了 B. 变小了 C. 不变 D. 无法确定
单选题 容易