1.
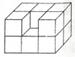
一个大正方体、四个中正方体、四个小正方体拼成如图的立体图形,已知大、中、小三个正方体的棱长分别为5厘米、2厘米、1厘米,那么,这个立体图形的表面积是平方厘米.

【考点】
组合体的表面积的巧算;
基础巩固
能力提升
变式训练
拓展培优
真题演练