1.
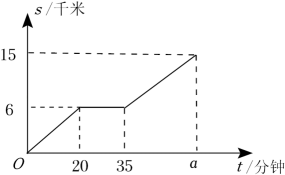
周末时,达瓦在体育公园骑自行车锻炼身体,他匀速骑行了一段时间后停车休息,之后继续以原来的速度骑行.路程s(单位:千米)与时间t(单位:分钟)的关系如图所示,则图中的a=.
【考点】
通过函数图象获取信息;
用图象表示变量间的关系;
基础巩固
能力提升
变式训练
拓展培优
真题演练