1.
综合与实践
动手操作:利用“正方形纸片的折叠和旋转”开展数学活动,探究体会图形在正方形折叠和旋转过程中的变化及其蕴含的数学思想方法.
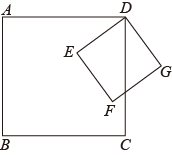
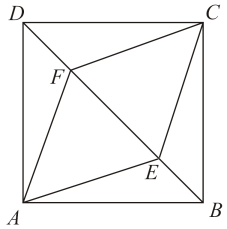
折一折:如图1,已知正方形ABCD的边长AB=6,将正方形ABCD沿过点A的直线折叠,使点B的对应点M落在AC上,展开正方形ABCD,折痕为AE,延长EM交CD于点F,连接AF.

(1)
思考探究:图1中,与△ABE全等的三角形有个,∠EAF=°,BE、EF、DF三者的数量关系是,BE的长为.
(2)
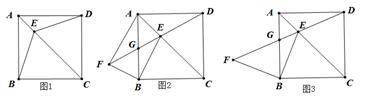
转一转:将图1中的∠EAF绕点A旋转到图2所示位置,与BC、CD的交点分别为E、F,连接EF.
(3)
开放拓展:如图3,在旋转∠EAF的过程中,当点F为CD的中点时,BE的长为.
证明推理:图2中,BE、EF、DF三者的数量关系是 ▲ , 并给出证明.
【考点】
勾股定理;
正方形的性质;
三角形全等的判定-SAS;