定义：我们把两条对角线互相垂直的四边形称为“垂美四边形”．

0 返回出卷网首页

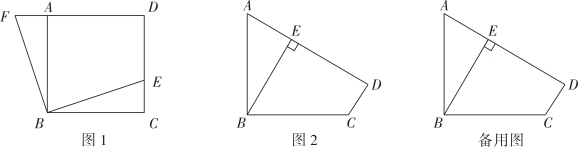
1. 定义：我们把两条对角线互相垂直的四边形称为“垂美四边形”．

(1) 特例感知：

如图1，四边形ABCD是“垂美四边形”，如果 $\text{[math]}$ ， OB=2， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ．

(2) 猜想论证

如图1，如果四边形ABCD是“垂美四边形”，猜想它的两组对边AB，CD与BC，AD之间的数量关系并给予证明．

(3) 拓展应用：

如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，∠BAC=60°，求GE长．

(4) 如图3，∠AOB=∠COD=90°，∠ABO=∠CDO=30°，∠BOC=120°，OA=OD， $\text{[math]}$ ，连接AC，BC，BD，请直接写出BC的长．

【考点】

相似三角形的判定与性质; 定义新运算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 阅读：三角形的一条边的平方等于另两条边的积，称这个三角形为优美三角形，这条边称为优美边.

(1) 已知 $\text{[math]}$ 是优美三角形，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长；

(2) 如图，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .求证： $\text{[math]}$ 是优美三角形.

综合题普通

2. 【定义】　数学活动课上，谢老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形．

(1) 【理解】如图1，已知A、B、C在格点（小正方形的顶点）上，请用两种不同的方法再画出一个格点D，使四边形ABCD为对等四边形；

(2) 如图2，在圆内接四边形ABCD中，AB是⊙O的直径，AC＝BD．试说明：四边形ABCD是对等四边形；

(3) 如图3，点D，B分别在x轴和y轴上，且B（0，3），∠BDO＝30°，点A是边BD上的一点，且AD：AB＝2，点C在x轴上，且四边形ABOC为对等四边形，请直接写出过点B、C、D的抛物线的解析式．

综合题困难

3. 从三角形（不是等腰三角形）一个顶点引一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．

(1) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的完美分割线，且 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

(2) 如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的完美分割线，且 $\text{[math]}$ 是以 $\text{[math]}$ 为底边的等腰三角形，找出 $\text{[math]}$ 与 $\text{[math]}$ 的关系．

综合题普通