1.
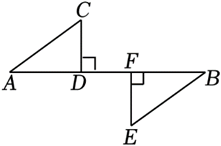
如图,已知 , 添加下列条件后不能使
, 添加下列条件后不能使 的是( )
的是( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
直角三角形全等的判定-HL;
三角形全等的判定-AAS;