1.
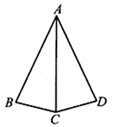
如图,已知 , 若
, 若 , 则
, 则 的度数为( )
的度数为( )

A.
80°
B.
90
C.
100°
D.
110
【考点】
三角形内角和定理;
三角形全等及其性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练