1.
(1)
【方法尝试】
(2)
【类比迁移】
(3)
【拓展延伸】
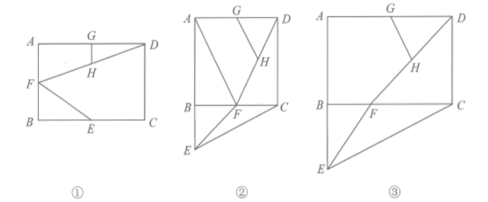
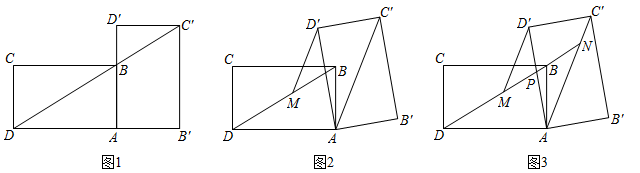
如图1,矩形是矩形
以点A为旋转中心,按逆时针方向旋转
所得的图形,
分别是它们的对角线.则
与
数量关系,位置关系;

如图2,在和
中,
. 将
绕点A在平面内逆时针旋转,设旋转角
为α(
),连接
. 请判断线段
和
的数量关系和位置关系,并说明理由;

如图3,在中,
, 过点A作
, 在射线
上取一点D,连接
, 使得
, 请求线段
的最大值.

【考点】
矩形的性质;
相似三角形的判定与性质;
旋转的性质;
能力提升
真题演练