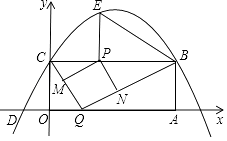
如图，在平面直角坐标系中，矩形的边，，点A在x轴的正半轴上，点C在y轴的负半轴上，抛物线经过A，C两点，连接.

0 返回出卷网首页

1. 如图，在平面直角坐标系 $\text{[math]}$ 中，矩形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ ，点A在x轴的正半轴上，点C在y轴的负半轴上，抛物线 $\text{[math]}$ 经过A，C两点，连接 $\text{[math]}$ .

(1) 请直接写出b，c的值；

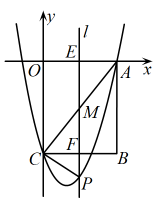
(2) 若动点 $\text{[math]}$ 在边 $\text{[math]}$ （不与O，A两点重合）上，过点E作x轴的垂线l交 $\text{[math]}$ 于点F，交 $\text{[math]}$ 于点M，交抛物线于点P，连接 $\text{[math]}$ .

①设线段 $\text{[math]}$ 的长为h，求h与m的函数关系式；

②当点P在 $\text{[math]}$ 下方的抛物线上时，以P，C，F为顶点的三角形与 $\text{[math]}$ 是否相似？若相似，请求出此时点E的坐标；若不相似，请说明理由.

【考点】

坐标与图形性质; 待定系数法求二次函数解析式; 线段上的两点间的距离; 矩形的性质; 相似三角形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，矩形OABC的两边在坐标轴上，点A的坐标为（10，0），抛物线y=ax²+bx+4过点B，C两点，且与x轴的一个交点为D（﹣2，0），点P是线段CB上的动点，设CP=t（0＜t＜10）．

(1) 请直接写出B、C两点的坐标及抛物线的解析式；

(2) 过点P作PE⊥BC，交抛物线于点E，连接BE，当t为何值时，∠PBE=∠OCD？

(3) 点Q是x轴上的动点，过点P作PM∥BQ，交CQ于点M，作PN∥CQ，交BQ于点N，当四边形PMQN为正方形时，请求出t的值．

综合题困难

2. 如图，抛物线W与x轴交于A(1，0)，M(﹣3，0)两点，交y轴于点B(0，3)，抛物线W关于y轴的对称图形为抛物线L.

(1) 求抛物线W的表达式；

(2) 如果E是点A关于原点的对称点，D是抛物线L的顶点，那么在x轴上是否存在点P，使得△PAD与△EBO是相似三角形？若存在，求出符合条件的点P坐标；若不存在，请说明理由.

综合题普通

3. 已知抛物线L： $\text{[math]}$ 过点 $\text{[math]}$ 和 $\text{[math]}$ ，与x轴的交点为A、B（点A在点B的左侧）.

(1) 求抛物线L的表达式；

(2) 若点P在抛物线L上，点E、F在抛物线L的对称轴上，D是抛物线L的顶点，要使 $\text{[math]}$ （P的对应点是D），且 $\text{[math]}$ .求满足条件的点P的坐标.

综合题普通