0 返回出卷网首页
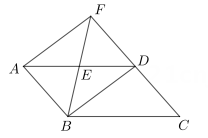
1. 如图，E、F是▱ABCD的对角线AC上的两点，且BE⊥AC，DF⊥AC，连接ED，FB.

(1) 求证：AE=CF．
(2) 连接BD交AC于点O，若BE＝4，EF＝6，求BD的长．
【考点】
勾股定理; 平行四边形的性质; 三角形全等的判定-AAS;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在方格纸中，A，B，C三点都在小方格的顶点上（每个小方格的边长为1）．

(1) 在图甲中画一个以A，B，C为其中三个顶点的平行四边形，并求出它的周长．

(2) 在图乙中画一个经过A，B，C三点的圆，并求出圆的面积．

综合题 普通
2. 如图，已知平行四边形 中， .

(1) 求平行四边形 的面积；
(2) 求证： .
综合题 普通
3. 如图1所示，在▱ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿射线AC的方向匀速平移得到△PNM，速度为1cm/s，同时，点Q从点C出发，沿射线CB方向匀速运动，速度为1cm/s，当△PNM停止平移时，点Q也停止运动，如图2所示，设运动时间为t（s）（0＜t＜4）．

(1) 当t为何值时，PQ∥MN？
(2) 设△QMC的面积为y（cm2），求y与t之间的函数关系式；
(3) 是否存在某一时刻t，使得PQ=QM，若存在，求出t的值；若不存在，请说明理由．
综合题 困难