已知 E在△ABC内部(如图①)，等边三角形ABC的边长为6，等边三角形BDE的边长为4，连结AE和DC

0 返回出卷网首页

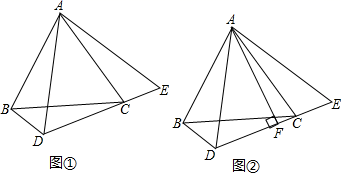
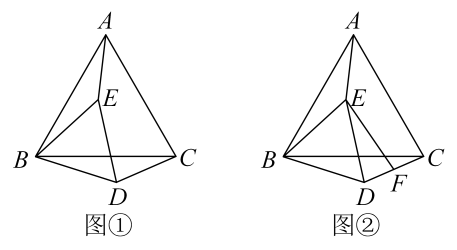
1. 已知 E在△ABC内部(如图①)，等边三角形ABC的边长为6，等边三角形BDE的边长为4，连结AE和DC

(1) 求证AE=DC；

(2) 当AE⊥BD时，求CD的长；

(3) 将△BDE绕点B旋转一周，F为DC的中点(如图②)，求旋转过程中EF的取值范围．

【考点】

等边三角形的性质; 勾股定理; 解直角三角形; 三角形全等的判定-SAS; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知△ABC是等边三角形，点D为平面内一点，连接DB、DC，∠BDC＝120°.

(1) 如图①，当点D在BC下方时，连接AD，延长DC到点E，使CE＝BD，连接AE.

①求证：△ABD≌△ACE；

②如图②，过点A作AF⊥DE于点F，直接写出线段AF、BD、DC间的数量关系；

(2) 若AB＝2 $\text{[math]}$ ，DC＝6，直接写出点A到直线BD的距离.

综合题普通

2. 如图， $\text{[math]}$ 是等边三角形，D是边AB上一点，以CD为边作E等边 $\text{[math]}$ ， DE交AC于点F，连接AE，

(1) 求证： $\text{[math]}$ ≌ $\text{[math]}$

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求CD的长.

综合题普通

3. 如图，在△ $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ 是 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ .

(1) 求证：△ $\text{[math]}$ ≌△ $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值.

综合题普通