1.
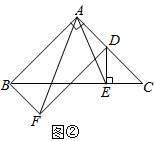
如图,在 ABCD中,AD=9cm,AB=3
ABCD中,AD=9cm,AB=3 cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)

(1)
求BC边上高AE的长度;
(2)
连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)
作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
【考点】
平行四边形的性质;
菱形的判定;
正方形的判定;
等腰直角三角形;
四边形-动点问题;
能力提升