1.
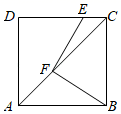
已知:在正方形ABCD中,点M是CD边上的任意一点,BE⊥AM于点E , DF⊥AM于点F .

(1)
求证: ADF≌
ADF≌ BAE;
(2)
如果正方形ABCD的边长为10,DF=6,求EF的长.
BAE;
(2)
如果正方形ABCD的边长为10,DF=6,求EF的长.
【考点】
勾股定理;
正方形的性质;
三角形全等的判定-AAS;