1.
如图，已知抛物线
经过点
， 与x轴交于点B、
．
(1)
求抛物线的顶点M的坐标；
(2)
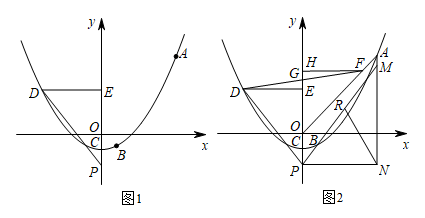
点E在抛物线的对称轴上，且位于x轴的上方，将
沿直线BE翻折，如果点C的对应点F恰好落在抛物线的对称轴上，求点E的坐标；
(3)
点P在抛物线的对称轴上，点Q是抛物线上位于第四象限内的点，当
为等边三角形时，求直线
的表达式．
【考点】
待定系数法求一次函数解析式;
待定系数法求二次函数解析式;
三角形全等及其性质;
