1.
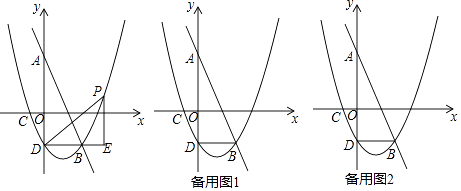
如图,抛物线 与x轴交于A,B两点,点A在点B的左侧,抛物线与y轴交于C,抛物线的顶点为D,直线
与x轴交于A,B两点,点A在点B的左侧,抛物线与y轴交于C,抛物线的顶点为D,直线 过点C交x轴于
过点C交x轴于 .
.

(1)
写出顶点D的坐标和直线 的解析式.
(2)
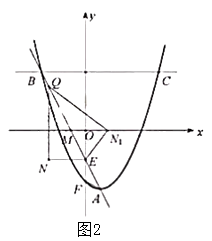
点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线
的解析式.
(2)
点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线 于M,交抛物线于N,连接
于M,交抛物线于N,连接 , 将
, 将 沿
沿 翻转,M的对应点为
翻转,M的对应点为 . 探究:是否存在点Q,使得
. 探究:是否存在点Q,使得 恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
【考点】
翻折变换(折叠问题);
二次函数与一次函数的综合应用;
能力提升
真题演练