1.
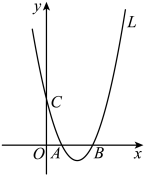
如图,抛物线 :
: 与
与 轴交于
轴交于 、
、 两点(点
两点(点 在点
在点 的左侧),与
的左侧),与 轴交于点
轴交于点 且
且 , 点
, 点 为抛物线
为抛物线 的对称轴右侧图象上的一点(不含顶点).
的对称轴右侧图象上的一点(不含顶点).
(1)
 的值为,抛物线的顶点坐标为;
(2)
设抛物线
的值为,抛物线的顶点坐标为;
(2)
设抛物线 在点
在点 和点
和点 之间的部分(含点
之间的部分(含点 和点
和点 )的最高点与最低点的纵坐标之差为
)的最高点与最低点的纵坐标之差为 , 求
, 求 关于
关于 的函数表达式,并写出自变量
的函数表达式,并写出自变量 的取值范围;
(3)
若点
的取值范围;
(3)
若点 的坐标满足
的坐标满足 时,连接
时,连接 , 将直线
, 将直线 与抛物线
与抛物线 围成的封闭图形记为
围成的封闭图形记为 .
.
①求点的坐标;
②直接写出封闭图形的边界上的整点(横、纵坐标都是整数)的个数.
【考点】
待定系数法求一次函数解析式;
待定系数法求二次函数解析式;
二次函数y=ax²+bx+c的性质;