1.
有些多项式的某些项可以通过适当地结合,(或把某项适当地拆分)成为一组,利用分组来分解多项式的因式,从而达到因式分解的目的,例如将 因式分解。
因式分解。
原式。
请在这种方法的启发下,解决以下问题:
(1)
分解因式 ;
(2)
;
(2)
 三边
三边 ,
,  ,
,  满足
满足 , 判断
, 判断 的形状,并说明理由。
(3)
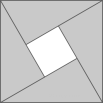
“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形,中间是一个小正方形。若直角三角形的两条直角边长分别是
的形状,并说明理由。
(3)
“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形,中间是一个小正方形。若直角三角形的两条直角边长分别是 和
和 , 斜边长是4,小正方形的面积是1。根据以上信息,先将
, 斜边长是4,小正方形的面积是1。根据以上信息,先将 因式分解,再求值。
因式分解,再求值。
【考点】
因式分解的应用;
等腰三角形的判定;
勾股定理;
能力提升


