1.
如图, 是
是 的中点.
的中点.

(1)
求证: ;
(2)
连接
;
(2)
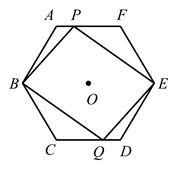
连接 , 在不添加辅助线的情况下,请直接写出与
, 在不添加辅助线的情况下,请直接写出与 面积相等的所有三角形.
面积相等的所有三角形.
【考点】
三角形的面积;
平行四边形的判定与性质;