如图，△ABC与△DCE中，CA＝CD ， ∠1＝∠2，BC＝EC ．

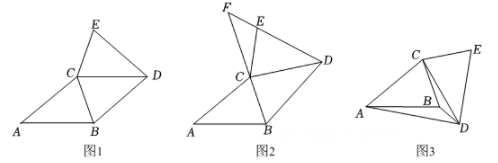
1. 如图，△ABC与△DCE中，CA＝CD ， ∠1＝∠2，BC＝EC ．

(1) 求证：∠A＝∠D ．

(2) 连接BE ， AD ，求证：∠CBE＝∠CAD ．

【考点】

等腰三角形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

解答题普通

解答题普通

3. 如图所示．在 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ， D是 $\text{[math]}$ 上的一点， $\text{[math]}$ ， $\text{[math]}$ ，点F为 $\text{[math]}$ 的中点．

求证：

解答题普通