1.
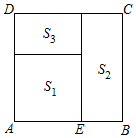
如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中P,连接PD,使得PF=PD,在AB的延长线上取点F,使PF以AF为边作正方形AMEF,点M在AD上.

(1)
AM,DM的长分别为 ,.
(2)
M是AD的黄金分割点吗?请说明理由.
【考点】
勾股定理;
正方形的性质;
黄金分割;