1.
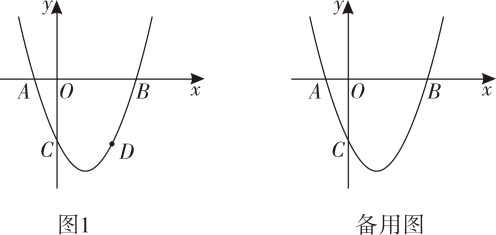
已知抛物线y=x2-(2m-1)x-2m的最低点的纵坐标为-4，它与x轴交于点A和B(点A在原点左侧，点B在原点右侧)，与y轴交于点C
(1)
求抛物线的解析式：
(2)
如图1，点D是抛物线的一点，与点C关于抛物线对称轴对称，点P(
n，kn+1)，n为任意实数，当n变化时，点P在直线l上运动，若点A，D到直线l的距离相等，求k的值；
(3)
将该抛物线在0≤x≤4间的部分记为图象G，将图象G在直线y=t下方的部分沿y=t翻折，其余部分保持不变，得到一个新的函数的图象，记这个函数的最大值为m，最小值为n，若m-n≤7．求t的取值范围．
【考点】
二次函数图象的几何变换;
待定系数法求二次函数解析式;
二次函数图象与坐标轴的交点问题;
三角形全等及其性质;
二次函数y=ax²+bx+c的性质;
能力提升
