1.
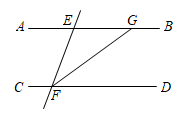
在一次数学实践探究活动中,小明和他的同伴们将两个直角三角尺按如图所示方式放置,发现了其中的奥秘.

(1)
如图①,已知 , 若
, 若 , 则
, 则 ;
(2)
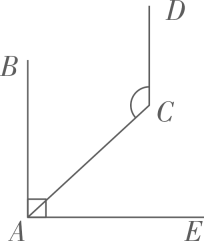
如图②,已知
;
(2)
如图②,已知 , 若
, 若 , 求
, 求 的度数;
(3)
经过一番探究,小明和他的同伴们发现:如图③,若
的度数;
(3)
经过一番探究,小明和他的同伴们发现:如图③,若 ,
,  , 则可以用含
, 则可以用含 和
和 的式子直接表示
的式子直接表示 的度数,你发现什么规律了吗?请你写出正确的结论,不必证明.
的度数,你发现什么规律了吗?请你写出正确的结论,不必证明.
【考点】
角的运算;