0 返回出卷网首页
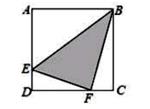
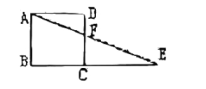
1. 如图所示，两个边长为6的正方形ABFE和CDEF拼成长方形ABCD．G为DE的中点．连接BG交EF于H．求图中五边形CDGHF的面积。

【考点】
三角形的面积; 正方形的面积;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
图形计算 普通
基础巩固
能力提升
变式训练
拓展培优
真题演练
换一批
1. 如图，已知BD＝5厘米，DC＝7厘米，E为AD的中点，△ABD的面积为12平方厘米。求△DEC的面积。
解答题 容易
2.

求阴影部分的面积（单位：cm）．

计算题 容易
3. 如图边长为 4 的正方形 ABCD 和边长为 6 的正方形 BEFG 并排放在一起，O1 和 O2 分别是两个正方形的中心（正方形对角线的交点），则阴影部分的面积是多少？
图形计算 容易