1.
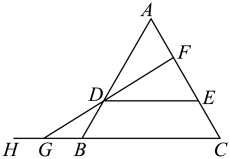
如图, ,
,  ,
,  ,
,  .
.

(1)
直线 与
与 有怎样的位置关系?并证明你的结论;
(2)
若
有怎样的位置关系?并证明你的结论;
(2)
若 , 求
, 求 的度数.
的度数.
【考点】
角的运算;
平行线的判定;
平行线的性质;
三角形的外角性质;
邻补角;