已知：如图，直线PQ∥MN，点C是PQ，MN之间（不在直线PQ，MN上）的一个动点．

0 返回出卷网首页

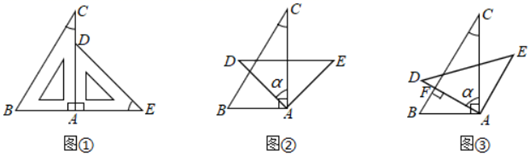
1. 已知：如图，直线PQ∥MN，点C是PQ，MN之间（不在直线PQ，MN上）的一个动点．

(1) 若∠1与∠2都是锐角，如图1，请直接写出∠C与∠1，∠2之间的数量关系．

(2) 若小明把一块三角板（∠A=30°，∠C=90°）如图2放置，点D，E，F是三角板的边与平行线的交点，若∠AEN=∠A，求∠BDF的度数．

(3) 将图2中的三角板进行适当转动，如图3，直角顶点C始终在两条平行线之间，点G 在线段CD上，连结EG，且有∠CEG=∠CEM， $\text{[math]}$ 的值是否变化？如果不变，求出比值；如果变化，请说明理由。

【考点】

角的运算; 平行公理及推论; 平行线的判定; 平行线的性质; 三角形内角和定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 一个长方形台球桌面 $\text{[math]}$ 如图1所示，已知台球在与台球桌边缘碰撞的过程中，撞击线路与桌边的夹角等于反弹线路与桌边的夹角，即图1中的 $\text{[math]}$ .

(1) 台球经过如图2所示的两次碰撞后，第二次的反弹线路为 $\text{[math]}$ .若开始时的撞击线路为 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(2) 台球桌因为长期使用，导致桌角松动变形如图3，在台球经过两次撞击之后，开始时的撞击线路EF所在直线与第二次的反弹线路 $\text{[math]}$ 所在直线相交于点M，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

综合题普通

2. 将一幅三角板如图①放置，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一条直线上，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，点 $\text{[math]}$ 为垂足， $\text{[math]}$ ， $\text{[math]}$ .

(1) 如图①， $\text{[math]}$ 的度数为， $\text{[math]}$ 的度数为；

(2) 若将三角板 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转角 $\text{[math]}$ .

①如图②，当旋转角 $\text{[math]}$ 等于45°时，试问 $\text{[math]}$ 吗？请说明理由；

②如图③，当 $\text{[math]}$ 于点 $\text{[math]}$ 时，请求出旋转角 $\text{[math]}$ 的度数.

综合题普通

3. 如图 1 所示，在三角形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边上一点，分别过点 $\text{[math]}$ 作 $\text{[math]}$ 的平行线交于点 $\text{[math]}$ ．

(1) 求 $\text{[math]}$ 的度数．

(2) 点 $\text{[math]}$ 为直线 $\text{[math]}$ 上的一个动点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，且 $\text{[math]}$ ，连结 $\text{[math]}$ ．
①如图 2 所示，当点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧，且 $\text{[math]}$ 时，判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由；
②在整个运动中，是否存在点 $\text{[math]}$ ，使得 $\text{[math]}$ ？若存在，请求出 $\text{[math]}$ 的度数，若不存在，请说明理由．

综合题普通