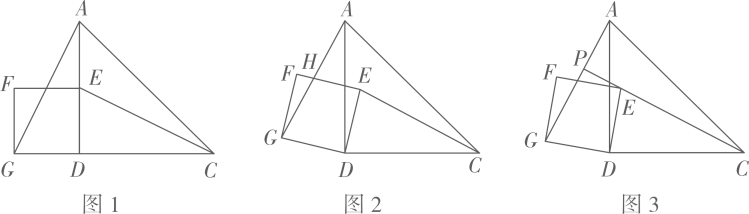
1.
数学中有一个定理叫做直角三角形斜边中线定理,它的内容是:直角三角形斜边上的中线等于斜边的一半.请同学们运用这个定理探究下面的数学问题:已知 和
和 都是等腰直角三角形,其中
都是等腰直角三角形,其中 ,
,  为
为 的中点,连接
的中点,连接 、
、 .
.

(1)
如图1,当 在
在 上,
上, 在
在 上时,线段
上时,线段 ,
,  的数量关系是;并且可以得到
的数量关系是;并且可以得到 (填度数).
(2)
在图1的基础之上,将
(填度数).
(2)
在图1的基础之上,将 绕点
绕点 顺时针旋转
顺时针旋转 得到图2,判断(1)中的结论是否仍然成立,并说明理由:
(3)
在图1的基础之上,将
得到图2,判断(1)中的结论是否仍然成立,并说明理由:
(3)
在图1的基础之上,将 绕点
绕点 顺时针旋转
顺时针旋转 得到图3,若
得到图3,若 , 求此时线段CF的长.
, 求此时线段CF的长.
【考点】
三角形全等及其性质;
勾股定理;
等腰直角三角形;