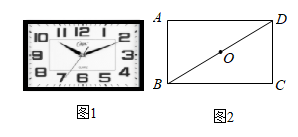1.
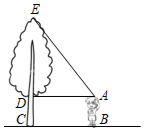
用某型号拖把去拖沙发底部地面的截面示意图如图所示,拖把头为矩形 ,
, 
 . 该沙发与地面的空隙为矩形
. 该沙发与地面的空隙为矩形 ,
,  ,
,  . 拖把杆为线段
. 拖把杆为线段 , 长为
, 长为 , O为
, O为 的中点,
的中点, 与
与 所成角
所成角 的可变范围是
的可变范围是 当
当 大小固定时,若
大小固定时,若 经过点G,或点A与点E重合,则此时
经过点G,或点A与点E重合,则此时 的长即为沙发底部可拖最大深度.
的长即为沙发底部可拖最大深度.

(1)
如图1,当 时,求沙发底部可拖最大深度
时,求沙发底部可拖最大深度 的长.(结果保留根号)
(2)
如图2,为了能将沙发底部地面拖干净,将α减小到
的长.(结果保留根号)
(2)
如图2,为了能将沙发底部地面拖干净,将α减小到 , 请通过计算,判断此时沙发底部可拖最大深度
, 请通过计算,判断此时沙发底部可拖最大深度 的长能否达到
的长能否达到 ?(
?( ,
,  )
)
【考点】
矩形的性质;
解直角三角形的其他实际应用;
能力提升
真题演练