1.
(1)问题探究:如图①,在 中,
中, ,
,  ,
,  , 点D是
, 点D是 的中点,点E是斜边
的中点,点E是斜边 上的任意一点,连接
上的任意一点,连接 , 请求出
, 请求出 的最小值.
的最小值.
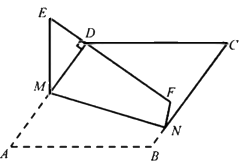
(2)问题解决:图②是某公园的一个五边形人工湖 , 已知
,
米,
米,
米,F为
中点,为更好地提升市民的观景体验,决定在湖中央修建一个半径为7.5米的观景台,并在人工湖上修建四条栈道
(宽度忽略不计),若修建栈道的造价为5000元/米,为节省资金,请问应如何设计使得修建栈道的费用最低,并求出最低费用.

【考点】
勾股定理;
相似三角形的判定与性质;
解直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练