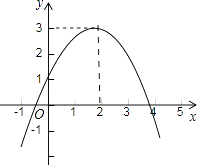1.
如图,在水平向右为 轴正方向,竖直向上为
轴正方向,竖直向上为 轴正方向的坐标系中标记了
轴正方向的坐标系中标记了 个格点,已知网格的单位长度为
个格点,已知网格的单位长度为 , 若二次函数
, 若二次函数 的图像经过其中的
的图像经过其中的 个格点,则
个格点,则 的最大值为( )
的最大值为( )

A.
 B.
1
C.
B.
1
C.
 D.
D.

【考点】
待定系数法求二次函数解析式;