1.
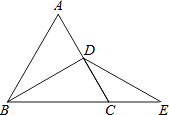
如图所示的是一款航模机翼部分示意图,已知 ,
,  ,
,  ,
,  , 请计算该机翼(四边形
, 请计算该机翼(四边形 的周长.(结果保留根号)
的周长.(结果保留根号)

【考点】
等腰三角形的判定与性质;
等边三角形的性质;
勾股定理;