1.
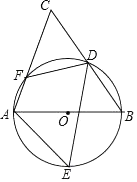
如图，AB是⊙O的直径，△ABC内接于⊙O ， 点I为△ABC的内心，连接CI并延长交⊙O于点D ， E是
上任意一点，连接AD ， BD ， BE ， CE ．
(1)
若∠ABC＝25°，求∠CEB的度数；
(2)
找出图中所有与DI相等的线段，并证明；
(3)
若CI＝2
， DI＝
， 求△ABC的周长．
【考点】
圆周角定理;
圆内接四边形的性质;
三角形的内切圆与内心;
解直角三角形;
切线长定理;
