1.
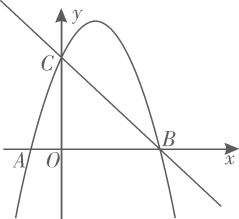
拋物线 与
与 轴交于点
轴交于点 和点
和点 (点
(点 在原点的左侧,点
在原点的左侧,点 在原点的右侧),与
在原点的右侧),与 轴交于点
轴交于点 .
.

(1)
求该拋物线的函数解析式;
(2)
如图1,直线 交抛物线于D,E两点,
交抛物线于D,E两点, 为抛物线顶点,连接PD,PE,若
为抛物线顶点,连接PD,PE,若 面积为
面积为 , 求
, 求 的值:
(3)
如图2,M,N是直线AC上的两个动点,
的值:
(3)
如图2,M,N是直线AC上的两个动点, 在
在 点左边且
点左边且 是直线下方抛物线上的点,
是直线下方抛物线上的点, , 求满足条件的
, 求满足条件的 点的横坐标.
点的横坐标.
【考点】
待定系数法求二次函数解析式;
三角形的面积;
勾股定理;
等腰直角三角形;
二次函数与一次函数的综合应用;