如图，在△ABC中，AB＝AC＝5，BC＝6．点D是边BC上的一点（点D不与点B、C重合），作射线AD ，在射线AD上取点P ，使AP＝BD ，以AP为边作正方形APMN ，使点M和点C在直线AD同侧．

0 返回出卷网首页

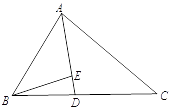
1. 如图，在△ABC中，AB＝AC＝5，BC＝6．点D是边BC上的一点（点D不与点B、C重合），作射线AD ，在射线AD上取点P ，使AP＝BD ，以AP为边作正方形APMN ，使点M和点C在直线AD同侧．

(1) 当点D是边BC的中点时，求AD的长；

(2) 当BD＝4时，点D到直线AC的距离为；

(3) 连结PN ，当PN⊥AC时，求正方形APMN的边长；

(4) 若点N到直线AC的距离是点M到直线AC距离的3倍，则CD的长为.（写出一个即可）

【考点】

三角形的面积; 等腰三角形的性质; 勾股定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，射线AM平行于射线BN，∠B=90°，AB=4，C是射线BN上的一个动点，连接AC，作CD⊥AC，且AC=2CD，过C作CE⊥BN交AD于点E，设BC长为a．

(1) 求△ACD的面积（用含a的代数式表示）；

(2) 求点D到射线BN的距离（用含有a的代数式表示）；

(3) 是否存在点C，使△ACE是以AE为腰的等腰三角形？若存在，请求出此时a的值；若不存在，请说明理由．

综合题困难

2. 已知：如图，在△ABC的中，AD是角平分线，E是AD上一点，且AB：AC=AE：AD．

求证：

(2) $\text{[math]}$

综合题普通

3. 问题探究

(1) 请在图①、图② 各作两条直线，使它们将正方形ABCD与半⊙O的面积三等分；

(2) 如图③，在矩形ABCD中，AB＝3，BC＝4，请在图③中过顶点A作两条直线，使它们将矩形ABCD的面积三等分，并说明理由；

问题解决

(3) 位于宝鸡市凤翔区的机场将计划于2024年建成通航．如图④，在机场旁边有一块平行四边形ABCD空地，其中AB＝AC＝100米，BC＝120米，根据视觉效果和花期特点，机场设计部门想在这块空地上种上等面积的三种不同的花，要求从入口点A处修两条笔直的小路（小路面积忽略不计）方便旅客赏花，两条小路将这块空地的面积三等分．那么设计部门能否实现自己的想法？若能实现，请通过计算，画图说明；若不能，请说明理由．

综合题普通