1.
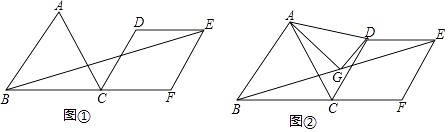
如图 1,把一个含  的直角三角板
的直角三角板  和一个正方形
和一个正方形  摆放在一起,使三角板的直角顶点和正方形的顶点
摆放在一起,使三角板的直角顶点和正方形的顶点  重合, 连接
重合, 连接  , 点
, 点  与
与  分别是
分别是  中点, 连接
中点, 连接  。
。

(1)
如图 1, 点  分别在正方形的边
分别在正方形的边  上, 连接
上, 连接  . 则
. 则  的数量关系是;
的数量关系是;  的位置关系是;
(2)
如图 2, 将图 1 中直角三角板
的位置关系是;
(2)
如图 2, 将图 1 中直角三角板  绕点
绕点  顺时针旋转, 当点
顺时针旋转, 当点  落在线段
落在线段  上时, 其他条件不变, (1) 中结论是否仍然成立, 若成立, 请证明结论, 若不成立, 请说明理由.
(3)
如图 3, 将图 1 中直角三角板
上时, 其他条件不变, (1) 中结论是否仍然成立, 若成立, 请证明结论, 若不成立, 请说明理由.
(3)
如图 3, 将图 1 中直角三角板  绕点
绕点  顺时针旋转
顺时针旋转  , 其他条件不变, 若
, 其他条件不变, 若  , 直接写出线段
, 直接写出线段  的最小值.
的最小值.
【考点】
平行线的性质;
三角形全等的判定;
勾股定理;
正方形的性质;
能力提升