如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB，AB，∠PBA=∠C．

0 返回出卷网首页

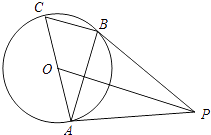
1. 如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB，AB，∠PBA=∠C．

(1) 求证：PB是⊙O的切线；

(2) 连接OP，若OP∥BC，且OP=8，⊙O的半径为2 $\text{[math]}$ ，求BC的长．

【考点】

平行线的性质; 圆周角定理; 切线的判定; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图， $\text{[math]}$ ，连 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，半径 $\text{[math]}$ 交 $\text{[math]}$ ， $\text{[math]}$ 于E ， F两点，延长 $\text{[math]}$ 至点G ，使得 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；

(3) 连 $\text{[math]}$ 交 $\text{[math]}$ 于点H ，若 $\text{[math]}$ 的半径为5， $\text{[math]}$ ，求 $\text{[math]}$ 的周长．

综合题困难

2. 如图，△ABC中，AB=AC，点D为BC上一点，且AD=DC，过A，B，D三点作⊙O，AE是⊙O的直径，连结DE．

(1) 求证：AC是⊙O的切线；

(2) 若sinC= $\text{[math]}$ ，AC=6，求⊙O的直径．

综合题普通

3. 如图，△ABC内接于⊙O，AB=AC，∠BAC=36°，过点A作AD∥BC，与∠ABC的平分线交于点D，BD与AC交于点E，与⊙O交于点F．

(1) 求∠DAF的度数；

(2) 求证：AE²=EF•ED；

(3) 求证：AD是⊙O的切线．

综合题普通