1.
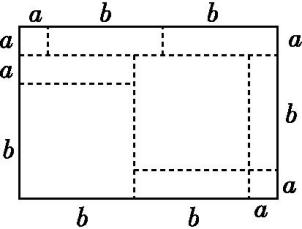
如图,将一张长方形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小长方形,且m>n.(以上长度单位:cm)
(1)观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 ;
(2)若每块小长方形的面积为10 cm2 , 四个正方形的面积和为58 cm2 , 试求图中所有裁剪线(虚线部分)长之和.

【考点】
因式分解的应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练