1.
双塔是古黄河宿迁景观带的标志性建筑之一,由九层的九龙塔和七层的七风塔构成.某校数学实践小组开展测量七凤塔高度的实践活动,该小组制定了测量方案,在实地测量后撰写活动报告,报告部分内容如表:
测量七凤塔高度 | |||
测量工具 | 测角仪、皮尺等 | 活动形式 | 以小组为单位 |
测量示意图 | 测量步骤及结果 | ||
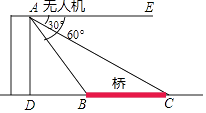
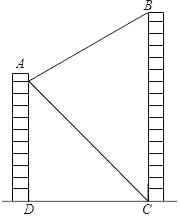
| 如图,步骤如下: ①在C处使用测角仪测得塔的顶部点B的仰角∠BDG=37°; ②沿着CA方向走到E处,用皮尺测得CE=24米; ③在E处使用测角仪测得塔的顶部点B的仰角∠BFG=45°. | ||
…… | |||
已知测角仪的高度为1.2米,点C、E、A在同一水平直线上.根据以上信息,求塔AB的高度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【考点】
解直角三角形的实际应用﹣仰角俯角问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练