1.
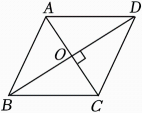
如图,在菱形 中,对角线
中,对角线 、
、 交于点
交于点 , 以
, 以 为斜边作
为斜边作 ,
,  与
与 交于点
交于点 , 连接
, 连接 , 使得
, 使得 , 且
, 且 , 若
, 若 , 则菱形
, 则菱形 的周长为( )
的周长为( )

A.
 B.
B.
 C.
C.
 D.
4
D.
4
【考点】
菱形的性质;