1.
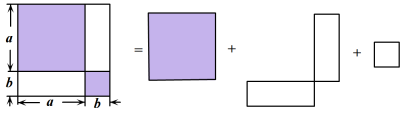
如图,C为线段 上的一点,分别以
上的一点,分别以 为边在
为边在 的两侧作正方形
的两侧作正方形 和正方形
和正方形 . 若
. 若 , 且两正方形的面积之和
, 且两正方形的面积之和 , 图中阴影部分面积为 .
, 图中阴影部分面积为 .

【考点】
完全平方公式的几何背景;
基础巩固
能力提升
变式训练
拓展培优
真题演练