已知二次函数y=ax2﹣8ax（a＜0）的图象与x轴的正半轴交于点A，它的顶点为P．点C为y轴正半轴上一点，直线AC与该图象的另一交点为B，与过点P且垂直于x轴的直线交于点D，且CB：AB=1：7．

0 返回出卷网首页

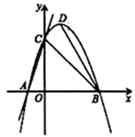
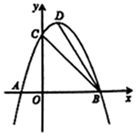
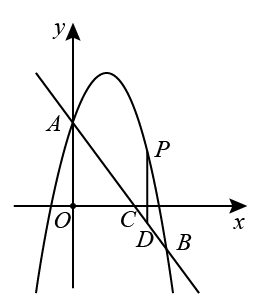
1. 已知二次函数y=ax²﹣8ax（a＜0）的图象与x轴的正半轴交于点A，它的顶点为P．点C为y轴正半轴上一点，直线AC与该图象的另一交点为B，与过点P且垂直于x轴的直线交于点D，且CB：AB=1：7．

(1) 求点A的坐标及点C的坐标（用含a的代数式表示）；

(2) 连接BP，若△BDP与△AOC相似（点O为原点），求此二次函数的关系式．

【考点】

相似三角形的判定与性质; 二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 在平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ ．

(1) 求抛物线顶点 $\text{[math]}$ 的坐标；（用含 $\text{[math]}$ 的代数式表示）

(2) 抛物线与 $\text{[math]}$ 轴只有一个公共点，经过点 $\text{[math]}$ 的直线与抛物线交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．

①判断 $\text{[math]}$ 的形状，并说明理由；

②已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，设 $\text{[math]}$ 的外心为点 $\text{[math]}$ ，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，求点 $\text{[math]}$ 的纵坐标 $\text{[math]}$ 的取值范围．

综合题困难

2. 在平面直角坐标系xOy中，如果抛物线 $\text{[math]}$ 上存在一点A，使点A关于坐标原点O的对称点 $\text{[math]}$ 也在这条抛物线上，那么我们把这条抛物线叫做回归抛物线，点A叫做这条抛物线的回归点.

(1) 已知点M在抛物线 $\text{[math]}$ 上，且点M的横坐标为2，试判断抛物线 $\text{[math]}$ 是否为回归抛物线，并说明理由；

(2) 已知点C为回归抛物线 $\text{[math]}$ 的顶点，如果点C是这条抛物线的回归点，求这条抛物线的表达式；

(3) 在（2）的条件下，所求得的抛物线的对称轴与x轴交于点D.连接CO并延长，交该抛物线于点E.点F是射线CD上一点，如果 $\text{[math]}$ ，求点F的坐标.

综合题普通

3. 如图，一条抛物线与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ， $\text{[math]}$ 为抛物线的顶点，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上.

(1) 求抛物线解析式；

(2) 若 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标；

(3) 过点 $\text{[math]}$ 作直线 $\text{[math]}$ 交抛物线于Q，是否存在以点A，P，Q，C为顶点的四边形是平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由；

(4) 坐标平面内一点M到点 $\text{[math]}$ 的距离为1个单位，求 $\text{[math]}$ 的最小值.

综合题困难