1.
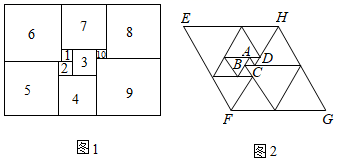
如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE和等边△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF、EF,则以下四个结论,正确的是( )
①△CDF≌△EBC;②∠CDF=∠EAF;③CG⊥AE;④△CEF是等边三角形.

A.
③④
B.
①②④
C.
①②③
D.
①②③④
【考点】
等边三角形的性质;
平行四边形的性质;
三角形全等的判定-SAS;