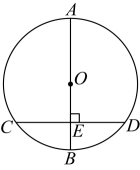石拱桥是我国古代人民勤劳和智慧的结晶（如图，隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为．桥的跨度（弧所对的弦长）m，设所在圆的圆心为，半径，垂足为．拱高（弧的中点到弦的距离）m．连接．求这座石拱桥主桥拱的半径．（精确到1m）．

0 返回出卷网首页

1. 石拱桥是我国古代人民勤劳和智慧的结晶（如图 $\text{[math]}$ ，隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为 $\text{[math]}$ ．桥的跨度（弧所对的弦长） $\text{[math]}$ m，设 $\text{[math]}$ 所在圆的圆心为 $\text{[math]}$ ，半径 $\text{[math]}$ ，垂足为 $\text{[math]}$ ．拱高（弧的中点到弦的距离） $\text{[math]}$ m．连接 $\text{[math]}$ ．求这座石拱桥主桥拱的半径．（精确到1m）．

【考点】

勾股定理; 垂径定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是直径， $\text{[math]}$ 是弦，且 $\text{[math]}$ 于点E ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．

解答题容易

2. 已知⊙O的弦AB长为10，半径长R为7，OC是弦AB的弦心距，求OC的长

解答题容易

3. 如图，水平放置的一条油管的截面半径为 $\text{[math]}$ ，其中有油部分油面宽 $\text{[math]}$ 为 $\text{[math]}$ ， $\text{[math]}$ 于点C，求截面上有油部分油面的高 $\text{[math]}$ ．

解答题容易