如图1，点C在y轴正半轴上，过点C作BC∥x轴，以BC为斜边作等腰直角△ABC ，使得直角顶点A恰好落在x轴正半轴上．已知B（a ， b），且a ， b满足：（a﹣8）2+|b﹣4|＝0．

0 返回出卷网首页

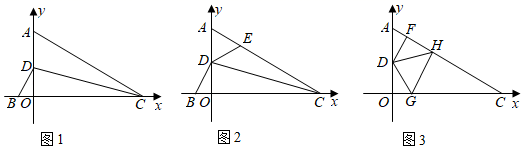
1. 如图1，点C在y轴正半轴上，过点C作BC∥x轴，以BC为斜边作等腰直角△ABC ，使得直角顶点A恰好落在x轴正半轴上．已知B（a ， b），且a ， b满足：（a﹣8）²+|b﹣4|＝0．

(1) 求点B坐标；

(2) 如图2，点D为AB的中点，连结CD ，过C作CE⊥CD且CE＝CD ，连接BE交AC于点N ，求 $\text{[math]}$ 的值；

(3) 如图3，若D点为等腰直角△ABC外部一点，∠CDB＝45°，连接DB交y轴于点E ， EF平分∠CEB交CB于F ．试判断∠CFE ， ∠CBD ， ∠CDB之间的数量关系，并说明理由．

【考点】

全等三角形的应用; 等腰直角三角形; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，点A、D在y轴正半轴上，点B、C分别在x轴上，CD平分∠ACB与y轴交于D点，∠CAO＝∠DBO．

(1) 求证：AC＝BC；

(2) 如图2，点C的坐标为（4，0），点E为AC上一点，且∠DEA＝∠DBO，求BC+EC的长；

(3) 在（1）中，过D作DF⊥AC于F点，点H为FC上一动点，点G为OC上一动点，（如图3），当H在FC上移动，点G在OC上移动时，始终满足∠GDH＝∠GDO+∠FDH，试判断FH、GH、OG这三者之间的数量关系，写出你的结论并加以证明．

综合题困难

2. 猜想与证明：小强想证明下面的问题：“有两个角（图中的 $\text{[math]}$ 和 $\text{[math]}$ ）相等的三角形是等腰三角形”．但他不小心将图弄脏了，只能看见图中的 $\text{[math]}$ 和边 $\text{[math]}$ ．

(1) 请问：他能够把图恢复成原来的样子吗？若能，请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子．

(2) 你能够证明这样的三角形是等腰三角形吗？（至少用两种方法证明）

综合题困难

3. 如图，平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ，以点 $\text{[math]}$ 为直角顶点在第二象限内作等腰 $\text{[math]}$ .

(1) 求点 $\text{[math]}$ 的坐标；

(2) 在 $\text{[math]}$ 轴右侧是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 全等？若存在，请求出点 $\text{[math]}$ 的坐标，若不存在，请说明理由.

综合题困难