1.
正面双手前掷实心球是发展学生力量和协调性的运动项目之一，实心球出手后的飞行路线可以看作是抛物线的一部分，建立如图所示的平面直角坐标系，从出手到着地的过程中，实心球的竖直高度
（单位：m）与水平距离
（单位：m）近似满足函数关系
． 小明进行了三次训练，令训练时实心球着地点到出手点的水平距离分别为
， 
， 
， （即三次训练的掷球成绩），若三次训练实心球所到达的最大高度相同，请回答以下问题：
(1)
第一次训练时，实心球的水平距离与竖直高度的几组数据如下：
(2)
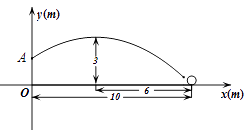
第二次训练时，实心球的竖直高度与水平距离的函数图象的一部分如图所示，其中
为第二次训练抛物线的顶点．
(3)
令第三次训练实心球到达最高点时，它与出手点的水平距离为
， 且第三次成绩介于前两次之间，则的取值范围是________．
水平距离 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
竖直高度 | 2 | 2.7 | 3.2 | 3.5 | 3.6 | 3.5 | 3.2 | 2.7 | 2 | 1.1 |
根据上述数据，则实心球到达最大高度是________m；
①结合图象及（1）中数据分析，直接判断的大小关系________；
②求出抛物线的解析式；
【考点】
待定系数法求二次函数解析式;
通过函数图象获取信息;
二次函数的实际应用-抛球问题;
能力提升
