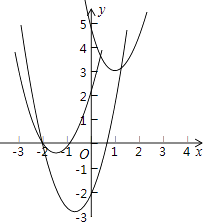如图，直线与轴交于点，与轴交于点，抛物线经过B，C两点，与轴另一交点为．点以每秒个单位长度的速度在线段BC上由点向点运动（点不与点和点重合），设运动时间为秒，过点作轴垂线交轴于点，交抛物线于点．

0 返回出卷网首页

1. 如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，抛物线 $\text{[math]}$ 经过B，C两点，与 $\text{[math]}$ 轴另一交点为 $\text{[math]}$ ．点 $\text{[math]}$ 以每秒 $\text{[math]}$ 个单位长度的速度在线段BC上由点 $\text{[math]}$ 向点 $\text{[math]}$ 运动（点 $\text{[math]}$ 不与点 $\text{[math]}$ 和点 $\text{[math]}$ 重合），设运动时间为 $\text{[math]}$ 秒，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴垂线交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，交抛物线于点 $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 如图①，过点P作y轴垂线交y轴于点N，连接MN交BC于点Q，当 $\text{[math]}$ 时，求t的值；

(3) 如图②，连接AM交BC于点D，当△PDM是等腰三角形时，直接写出t的值．

【考点】

待定系数法求一次函数解析式; 待定系数法求二次函数解析式; 等腰三角形的性质; 解直角三角形; 相似三角形的性质-对应边;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知在△ABC中，AB=AC，tan∠B=2，BC=4，D为BC边的中点，点E在BC边的延长线上，且CE=BC，连接AE，F为线段AE的中点

(1) 求线段CF的长；

(2) 求∠CAE的正弦值．

综合题普通

2. 如图，在平面直角坐标系xOy中，已知抛物线y= $\text{[math]}$ 与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，﹣3），经过点A的射线AM与y轴相交于点E，与抛物线的另一个交点为F，且 $\text{[math]}$ .

(1) 求这条抛物线的表达式，并写出它的对称轴；

(2) 求∠FAB的余切值；

(3) 点D是点C关于抛物线对称轴的对称点，点P是y轴上一点，且∠AFP=∠DAB，求点P的坐标．

综合题困难

3. 如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax²+bx+5经过点M（1，3）和N（3，5）

(1) 试判断该抛物线与x轴交点的情况；

(2) 平移这条抛物线，使平移后的抛物线经过点A（﹣2，0），且与y轴交于点B，同时满足以A、O、B为顶点的三角形是等腰直角三角形，请你写出平移过程，并说明理由．

综合题普通