1.
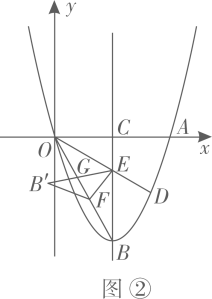
如图，在平面直角坐标系xOy中，已知抛物线y= 
与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，﹣3），经过点A的射线AM与y轴相交于点E，与抛物线的另一个交点为F，且 
.
(1)
求这条抛物线的表达式，并写出它的对称轴；
(2)
求∠FAB的余切值；
(3)
点D是点C关于抛物线对称轴的对称点，点P是y轴上一点，且∠AFP=∠DAB，求点P的坐标．
【考点】
待定系数法求二次函数解析式;
解直角三角形;
